集体智慧编程-01~02-导读与推荐系统
约定:
笔者本人读书笔记的行文风格,比较喜欢使用QA,采用一问一答的方式来进行学习。学习知识也并不完全是线性的我会在讲解一些具体复杂的概念之前先提出or讲解若干个知识点,来帮助大家进行学习,所以就算是零基础 没有数理统计(线性代数、离散数学、概率论)等背景的同学也应该可以看懂,如果有问题,大家的Question放在评论区我觉得必要的内容会补充到学习问题前的知识点内容里面
基本代码运行环境是 macos 、python3.10.12版本。
特别声明:部分代码由gpt4直接生成
A、导读
Q1、什么是集体智慧编程
- 集体智慧并不是说群体意识或者超自然现象
- 集体智慧编程 实际上是指 把一群人的行为特征 通过使用数据统计、机器学习算法的手段 总结整理或者抽象为一种可以被利用的模型,比较常见的比如说google的排序,很多人有更好评价的网页会被google放在前面
- 集体智慧 也可以是 整理汇总一群人的思想和知识 协作去解决某类问题,比如大家一起编辑的百度百科
Q2、什么是机器学习
简单来说 机器学习的核心是被计算出来的数学公式。当然这样描述可能太过简单了,他的核心功能是 从数据中学习规律和模式,以此来做出预测或决策,但是不管是什么功能,他的判断或者说决策逻辑都是依赖于通过大量训练集训练出的模型参数,这些模型参数为了方便理解 我们就认为是 下面这个方程里面的a和b吧,训练的过程就是不断去计算调整a和b的过程
$$
f(x) = ax+b
$$机器学习的算法通常用两种,一种是比较直观或者说可解释的,比如说 决策树,还有一些因为参数太多了 内部计算逻辑过于复杂,我们能够观察到的就是我们输入了什么样的数据,它最终有什么样的输出,计算过程对于我们来说是比较黑盒的,比如说 神经网络,关于神经网络和多层神经网络 我们后面的文章会详细去了解这部分内容
B、提供推荐
Q1、基本推荐系统的构成要素应该有哪些
个人认为可以核心应该是以下三个部分
- 候选集
- 你可理解 根据某种算法 从当前站内所有的内容里面挑选一部分可能和你相关的内容,后面所有的你可能看到的内容都是来自于这个集合
- 过滤
- 从候选集合中采用一定的算法规则进行批量的过滤
- 排序
- 排序一般决定就是过滤之后的你看到的内容顺序了
- 候选集
除此之外 还有一些工程性的模块
- 收集(冷启动)
- 提前采集用户信息,还有站内内容信心,为后续的候选集、过滤、排序服务
- 评估
- 评估召回结果的准确率,推荐的匹配率等信息
- 反馈
- 用户反馈反过来调整算法模型(当然一般是T+N的模式)
一个最基本的架构如下图所示:
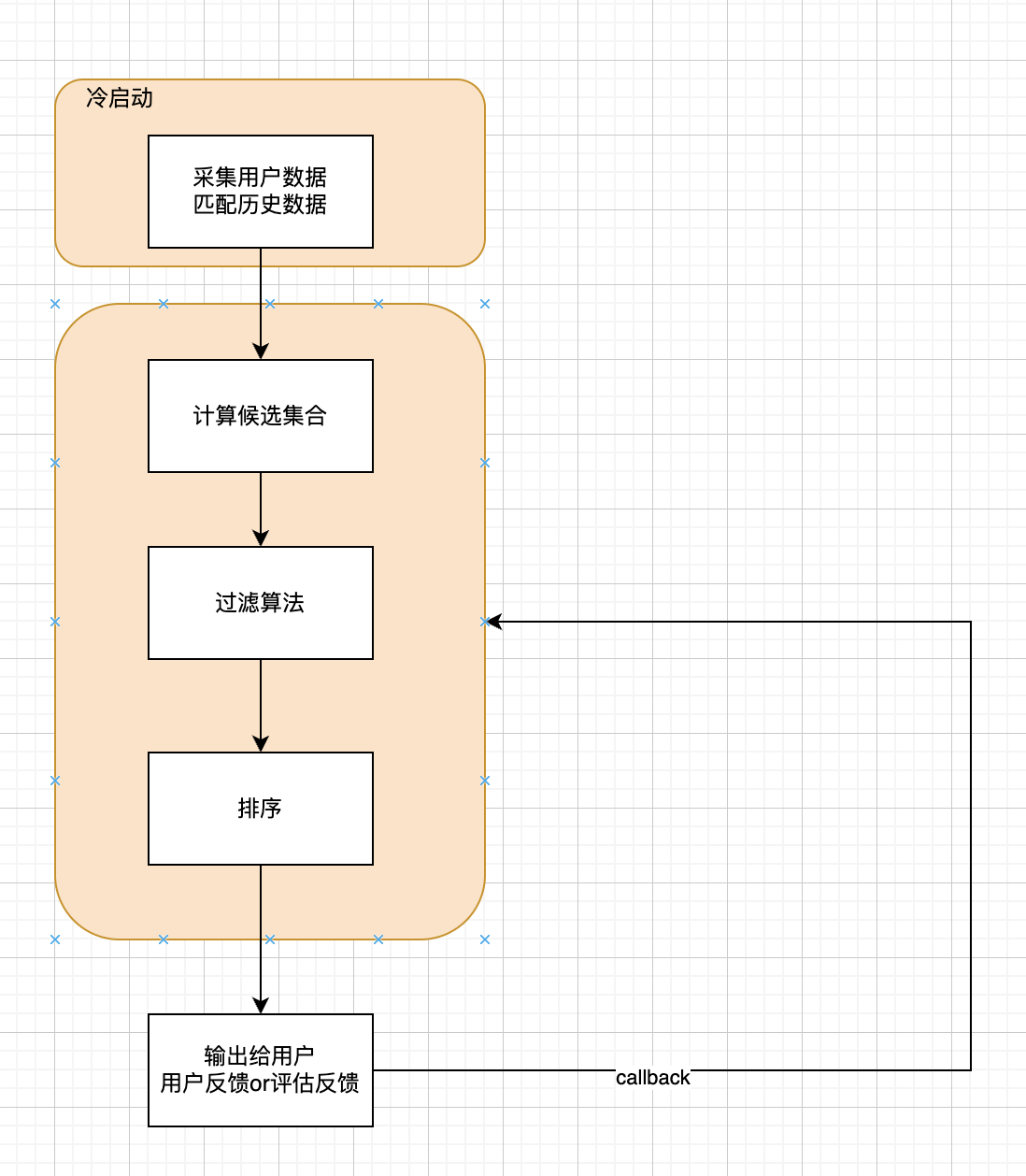
Q2、如何计算候选集
这个问题的细节非常的复杂,我这里暂时不做详细解释
基于内容的推荐
- 用户特征匹配
- 根据用户过去喜欢或与之互动的物品的内容特征,如物品的类别、标签、描述等,找到具有相似特征的内容作为候选集。
- 用户画像
- 用户的兴趣、偏好的属性等,然后选择与用户画像匹配度高的内容
- 用户特征匹配
协同过滤
- 用户-用户 协同过滤
- 根据你好朋友的一些推荐,来给你进行推荐,所以就很可能出现你的朋友刚刷到的视频,你立刻刷到了的情况
- 物品-物品 协同过滤
- 在pdd买过东西的应该都知道,pdd的搜索推荐能力非常强,基本上除非你命中黑名单词库,不然总是能给你推荐一些和你过去购买的物品很类似的东西给你,就算是你搜的和这个东西完全不相关
- 用户-用户 协同过滤
基于规则的方法
- 一般来说我们常说的推荐工程测的同学,就是在这个地方做工,举个最简单的例子,产品提一个需求,要求计算候选集合的时候给所有的人的候选集合中添加一批 站内高价值内容 就需要在候选集这个地方进行一定的改造。
基于模型的方法
矩阵分解
这个比较常用的一个方法是SVD,这个解释起来比较麻烦,我尽量用简单语言来描述
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23#假设有一个用户-物品评分矩阵,其中行代表用户,列代表物品,矩阵的值代表用户对物品的评分。在实际情况中,这样的矩阵通常是稀疏的,因为不是每个用户都对所有物品进行评分。根据下面的这个我们可以得到三个矩阵,之后我们可以根据这三个矩阵去计算用户的一些隐形偏好,比如 用户1从来没有对物品3进行打分,那么我们可以通过一定的数学手段结合这三个矩阵去算用户1对物品3的偏好程度
import numpy as np
from scipy.linalg import svd
# 构造上述评分矩阵,未知评分用0代替
R = np.array([
[5, 3, 0, 1],
[4, 0, 0, 1],
[1, 1, 0, 5],
[1, 0, 5, 4]
])
# 进行SVD分解
U, sigma, VT = svd(R, full_matrices=False)
(array([[-0.51988645, -0.64437991, 0.12678468, -0.54627672],
[-0.36357823, -0.38059565, 0.16697705, 0.83371247],
[-0.49580083, 0.19734636, -0.84462058, 0.04303526],
[-0.59305184, 0.63322658, 0.49260571, -0.06821454]]),
array([8.50590985, 5.88029226, 3.31987438, 1.74645202]),
array([[-0.60459115, -0.24165083, -0.34861164, -0.67419903],
[-0.66556372, -0.29518828, 0.53843121, 0.42424125],
[ 0.2861002 , -0.13984461, 0.74190415, -0.59005796],
[ 0.33112104, -0.91373532, -0.19529462, 0.13155466]]))
深度学习网络
- 使用比如CNN,RNN模型 对用户的历史以及物品的特征进行过滤
Q3、协同过滤的实际应用 (CF算法)
CF算法的核心是处理 user-item矩阵,举个简单的例子,你是A,我通过分析你的历史记录,发现有一个和你消费习惯很像的 B,我就把一些曝光给B,并且B购买了的商品推荐给你,这样做有几个好处:
- 简单,使用范围广,只依赖历史数据。
- 能得到长尾item
- 往往比较worker,能有比较好的效果
同样也有一些坏处:
- 初次启动需要大量的冷启动数据
- 解释性不强
协同过滤常见的实现方式
当我们拿到经过协同过滤的数据之后,我们就可以根据用户相似度权重以及他们对物品的偏好,预测当前用户没有偏好的未涉及物品,计算得到一个排序的物品列表作为推荐
Q4、数据之间的距离度量
这里有个延伸概念,就是如何计算用户的相似度
- 欧几里得距离:比如我们可以有一个用户叫做toby 他对物品A snakes 是4.5分,对物品B Durpree的评分是1分,那么我们就以此为坐标建立用户Toby、Lasalle 等对Snake和Durpree的偏好空间,然后计算距离就可以了 也就是 下面这个公式,这个原理是很好解释的。
$$
f(x)= \sqrt{(x_1^2 - x_2^2)+(y_1^2-y_2^2)}
$$
- 欧几里得距离:比如我们可以有一个用户叫做toby 他对物品A snakes 是4.5分,对物品B Durpree的评分是1分,那么我们就以此为坐标建立用户Toby、Lasalle 等对Snake和Durpree的偏好空间,然后计算距离就可以了 也就是 下面这个公式,这个原理是很好解释的。

-
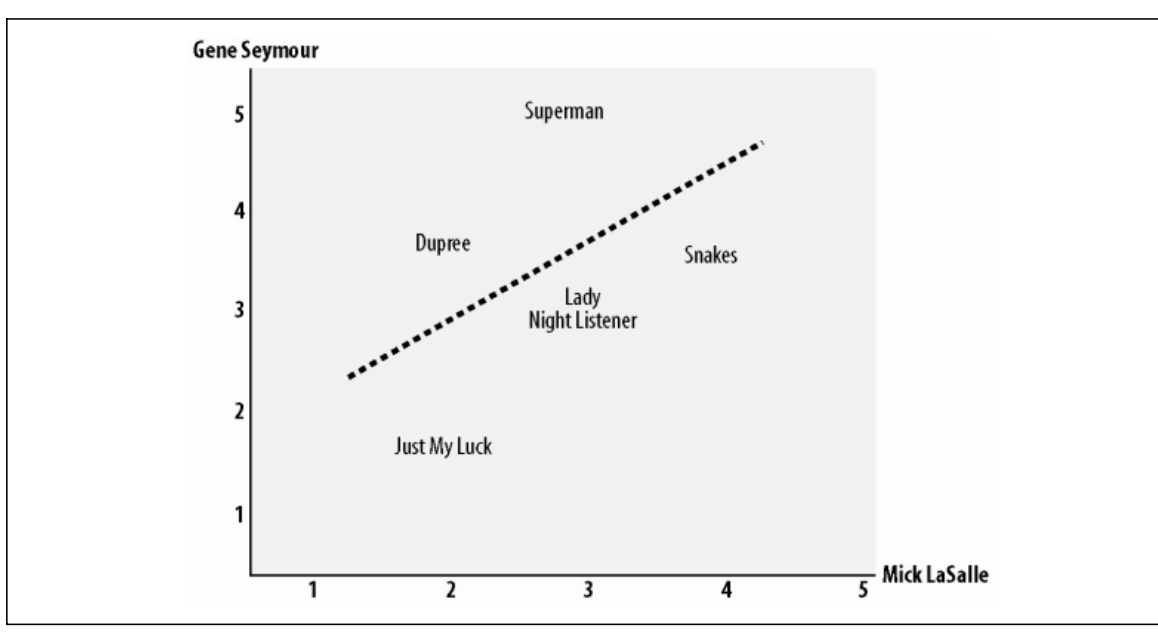
- 皮尔逊相关系数
- 简单来说这个是断两组数据与某一直线拟合程度的一种度量,比如之前上一张图的横纵坐标是物品,而皮尔逊系数则是两个人对五个物品的评分组成了他们的横纵坐标,一般来说点越靠近这跟直线,那么这两个人的品味我们就可以近似的理解更相似,其实要想搞明白这个系数 我们需要首先去理解协方差相关的概念,这里还是直接引用高质量的文章来为大家详细介绍皮尔逊相关系数:https://blog.csdn.net/huangfei711/article/details/78456165
- 收集(冷启动)